When Solar Radiation Corrupts Flight-Control Data: Why Hamming Codes Matter More Than Ever
Last week Airbus published a precautionary fleet notice for the A320 family.
Inside the document, one highlighted sentence caught my attention:
Airbus press released related to malfuntioning in A320 aircraft
“Analysis of a recent event involving an A320 Family aircraft has revealed that intense solar radiation may corrupt data critical to the functioning of flight controls.”
(Airbus Press Release, 28 November 2025)
A major flight-control anomaly attributed to radiation-induced data corruption.
If this can happen inside a commercial airliner — with shielding, certification, and redundancy — imagine what happens inside a satellite, orbiting deep within a harsh radiation environment. This is a real example of a Single Event Effect like the ones we experience in space systems.
This article uses that event as a springboard to explain something every aerospace engineer must understand:
How Hamming Codes protect RAM from radiation-induced bit flips.
Case Study: If Radiation Can Flip Aircraft Data… What Happens on a Satellite?
Let’s simplify the Airbus scenario into something concrete.
Imagine the corrupted flight-control data was nothing more than:
altitude_reference = 10000
stored in RAM.
A cosmic ray changes one bit in that variable.
Suddenly:
10000 turns into 8384
or 9472
or 9984
This is exactly what happens when RAM is unprotected.
Now let’s learn how Hamming codes would change that.
Hamming Codes Explained — The Real Goal of This Article
Hamming codes were invented by Richard Hamming in 1950 to solve one problem: How can a computer automatically fix a corrupted bit and keep running safely?
The brilliance of Hamming codes lies in two ideas:
Add redundant parity bits in carefully chosen positions
Use those bits to identify the exact position of a flipped bit
No trial-and-error. No human intervention. No guesswork.
Let’s walk through how they work.
1. Hamming Places Parity Bits at Power-of-Two Positions
For an 8-bit value, Hamming typically stores:
8 data bits
4 parity bits
The parity bits go in positions:
1, 2, 4, 8
Why these positions? Because each parity bit checks a specific combination of bits that allows the system to triangulate exactly which one flipped.
Think of each parity bit as asking a question:
p1: “Is the parity wrong among bits I cover?”
p2: “Is the parity wrong among my group?”
p4: “Is the parity wrong among my group?”
p8: “Is the parity wrong among my group?”
If one of them flips, the system now has enough information to locate the error.
2. Every Parity Bit Checks a Different Pattern
For example, parity bit p1 checks bits:
1, 3, 5, 7, 9, 11
Parity bit p2 checks:
2, 3, 6, 7, 10, 11
Parity bit p4 checks:
4, 5, 6, 7, 12
Parity bit p8 checks:
8, 9, 10, 11, 12
These overlapping patterns are chosen so that every single bit in the codeword has a unique “signature” of which parity groups it belongs to.
This is the key.
3. Detecting Where the Error Occurred: The Syndrome
When the system reads the stored value:
It recalculates all parity bits
It compares them to the stored parity bits
Each mismatch contributes a “1” to a binary number called the syndrome
Example:
p1 mismatch → contributes 1
p2 mismatch → contributes 2
p4 mismatch → contributes 4
p8 mismatch → contributes 8
Add them up and you get…
syndrome = position_of_flipped_bit
This is the genius of Hamming — the parity mismatches literally encode the bit index.
If bit 7 flipped, the syndrome will be:
p1 mismatch → 1
p2 mismatch → 2
p4 mismatch → 4
p8 match → 0
--------------------
1 + 2 + 4 = 7
The software knows exactly which bit to correct.
4. Correction Is Automatic
Once the syndrome reveals the flipped bit:
the system flips it back
the data is restored
the CPU receives uncorrupted data
This can be done in hardware, software, or both — but the key is that it is automatic.
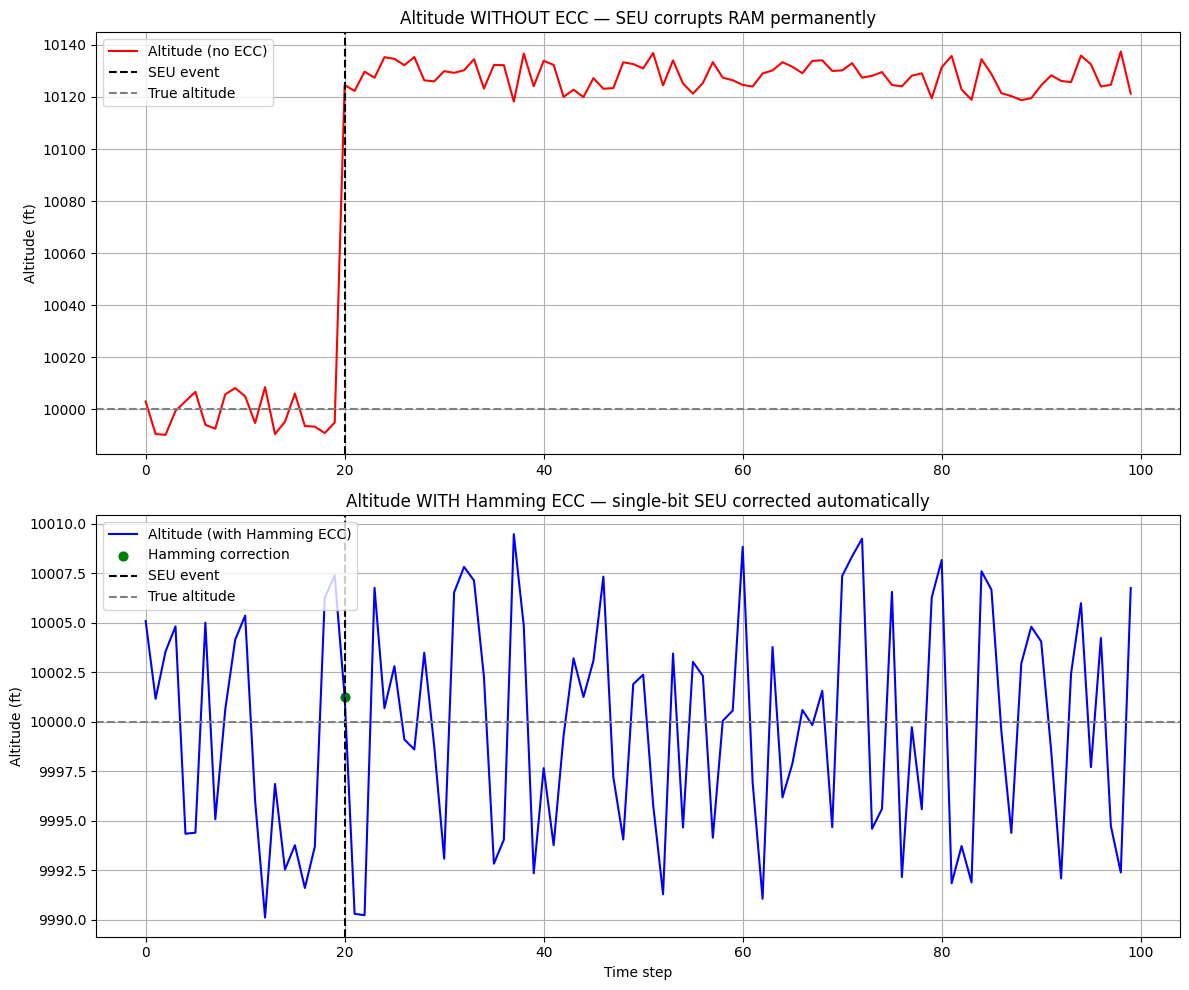
Let’s Demonstrate This With Code
We simulated two cases:
Without Hamming (raw RAM)
A single SEU corrupts the altitude permanently. The system reads and uses the wrong value indefinitely.
With Hamming ECC
A SEU flips a bit in the codeword.
On the next read:
✓ parity bits are recalculated
✓ syndrome indicates the wrong bit
✓ software corrects it instantly
The plot shows a single green correction point — and then the system continues normally.
Output from the presented program comparing the case without error correction and with it.
🔗 Link to the simulation code:
https://colab.research.google.com/drive/1Y-f_ln-zgl3BvBbbbif4Im7kLPXjVlbh?usp=sharing
One Important Limitation: Hamming Fixes One Bit Only
Pure Hamming codes (without extensions) can:
✓ correct one bit
✗ detect but not correct two simultaneous bit flips
This means:
A single SEU → automatically repaired
Two SEUs in the same codeword → Hamming cannot fix them
This is the perfect segue into the next article, where we’ll explore how to detect double-bit errors and extend Hamming codes into industrial-grade protection.
Try It Yourself in the Code
In the simulation notebook:
Change the SEU injection to flip two bits
Observe how:
the unprotected version collapses
the Hamming version detects something is wrong but cannot repair it
This is the best way to feel the strengths and limits of pure Hamming coding.
Final Thoughts
The Airbus report is a real-world reminder that a single flipped bit can disrupt flight-critical systems.
In satellites — it can be mission-ending.
But using Hamming memory protection requires:
4 extra bits for every 8 data bits (≈50% overhead)
additional processing time to compute parity and syndrome
The final decision should always consider the mission’s constraints and the criticality of the process.
But Hamming codes remain one of the most elegant, efficient, and essential layers of protection against radiation-induced failures.
And understanding them deeply is necessary for anyone entering the space electronics world.
